Cho hàm số $y=f(x)$ liên tục trên $\mathbb{R}$ và $\displaystyle\int\limits_{-1}^1 \frac{f(x)+f(-x)}{2018^x+1}\mathrm{\,d}x=2018$. Tính tích phân $\displaystyle\int\limits_{-1}^1 f(x)\mathrm{\,d}x=2018$.
A.
$2017$
B.
$2018$
C.
$1009$
D.
$0$
Đáp án và lời giải
Đáp án:B
Lời giải:Xét $I=\displaystyle\int\limits_{-1}^1 \frac{f(x)+f(-x)}{2018^x+1}\mathrm{\,d}x$. Đổi biến $x=-t$ ta được $$I=\displaystyle\int\limits_{-1}^1 \frac{2018^t(f(t)+f(-t))}{2018^x+1}\mathrm{\,d}t =\displaystyle\int\limits_{-1}^1 \frac{2018^x(f(x)+f(-x))}{2018^x+1}\mathrm{\,d}x.$$ Từ đó ta có $$ I=\frac{1}{2}\left[\displaystyle\int\limits_{-1}^1 \frac{f(x)+f(-x)}{2018^x+1}\mathrm{\,d}x+ \displaystyle\int\limits_{-1}^1 \frac{2018^x(f(x)+f(-x))}{2018^x+1}\mathrm{\,d}x \right]=\displaystyle\int\limits_{-1}^1 [f(x)+f(-x)]\mathrm{\,d}x=2018 .$$ Xét $J=\displaystyle\int\limits_{-1}^1 f(x)\mathrm{\,d}x$, đổi biến $x=-t$ ta được $J=\displaystyle\int\limits_{-1}^1 f(-x)\mathrm{\,d}x$ nên $$ J=\frac{1}{2}\displaystyle\int\limits_{-1}^1 [f(x)+f(-x)]\mathrm{\,d}x=2018. $$

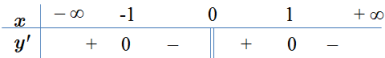 Mệnh đề nào dưới đây sai?
Mệnh đề nào dưới đây sai?