Nội dung bài giảng
Bài 1. Vẽ đồ thị của các hàm số:
a) \(y = 4^x\);
b) \(y= \left ( \frac{1}{4} \right )^{x}\).
Hướng dẫn giải:
a) Đồ thị hàm số \(y = 4^x\)
Tập xác định: \(\mathbb R\)
Sự biến thiên:
\(y' = {4^x}\ln 4 > 0,\forall x \in \mathbb R\)
- Hàm số đồng biến trên \(\mathbb R\)
- Giới hạn đặc biệt:
\(\eqalign{
& \mathop {\lim }\limits_{x \to - \infty } y = 0 \cr
& \mathop {\lim }\limits_{x \to + \infty } y = + \infty \cr} \)
Tiệm cận ngang: \(y=0\)
- Bảng biến thiên:
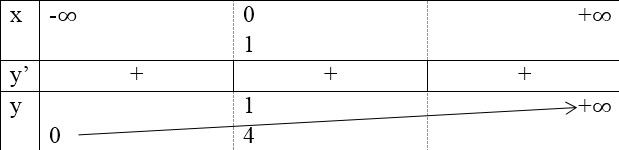
Đồ thị:
Đồ thị nằm hoàn toàn phía trên trục hoành, cắt trục tung tại các điểm \((0;1)\), đi qua điểm \((1;4)\) và qua các điểm \((\frac{1}{2}; 2)\), \((-\frac{1}{2}; \frac{1}{2})\), \((-1; \frac{1}{4})\).
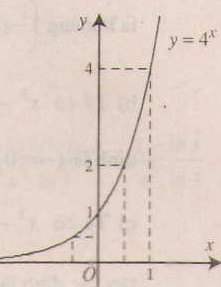
b) Đồ thị hàm số \(y=\left ( \frac{1}{4} \right )^{x}\)
Tập xác định: \(\mathbb R\)
Sự biến thiên:
\(y' = - {\left( {{1 \over 4}} \right)^x}\ln 4 < 0,\forall x \in \mathbb R\)
- Hàm số nghịch biến trên \(\mathbb R\)
- Giới hạn:
\(\eqalign{
& \mathop {\lim }\limits_{x \to - \infty } y = + \infty \cr
& \mathop {\lim }\limits_{x \to + \infty } y = 0 \cr} \)
Tiệm cận ngang \(y=0\)
- Bảng biến thiên:
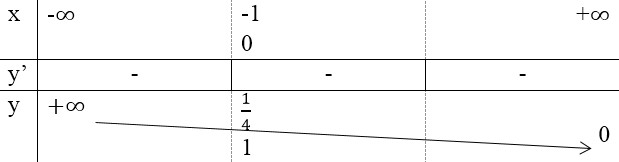
Đồ thị:
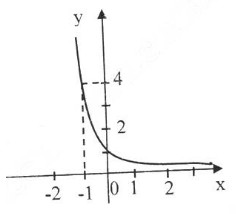
Đồ thị hàm số nằm hoàn toàn về phía trên trục hoành, cắt trục tung tại điểm (0; 1), đi qua điểm (1; \(\frac{1}{4}\)) và qua các điểm (\(-\frac{1}{2}\); 2), (-1;4).

