Nội dung bài giảng
Bài 42. Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
a)\(y = {1 \over 3}{x^3} - {x^2} - 3x - {5 \over 3}\)
b) \(y = {x^3} - 3x + 1\)
c) \(y = - {1 \over 3}{x^3} + {x^2} - 2x - {2 \over 3}\)
d) \(y = {x^3} - 3{x^2} + 3x + 1\)
Gỉải
a) TXĐ: \(D =\mathbb R\)
\(\eqalign{
& \mathop {\lim }\limits_{x \to + \infty } y = + \infty ;\,\,\mathop {\lim }\limits_{x \to - \infty } y = - \infty \cr
& y' = {x^2} - 2x - 3;\,\,y' = 0 \Leftrightarrow \left[ \matrix{
x = - 1 \hfill \cr
x = 3 \hfill \cr} \right.;\,\,y\left( { - 1} \right) = 0;\,\,y\left( 3 \right) = {{ - 32} \over 3} \cr} \)
Bảng biến thiên:

\(y'' = 2x - 2;\,y'' = 0 \Leftrightarrow x = 1;\,y\left( 1 \right) = - {{16} \over 3}\)
Xét dấu y”
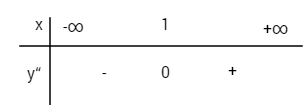
Điểm uốn \(I\left( {1; - {{16} \over 3}} \right)\)
Điểm đặc biệt: \(x = 0 \Rightarrow y = {{ - 5} \over 3}\)
Đồ thị: Đồ thị nhận \(I\left( {1; - {{16} \over 3}} \right)\) làm tâm đối xứng.

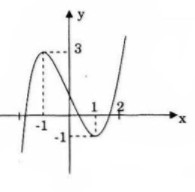
b) TXĐ: \(D =\mathbb R\)
\(\eqalign{
& \mathop {\lim }\limits_{x \to + \infty } y = + \infty ;\,\mathop {\lim }\limits_{x \to - \infty } y = - \infty \cr
& y' = 3{x^2} - 3;\,y' = 0 \Leftrightarrow \left[ \matrix{
x = - 1 \hfill \cr
x = 1 \hfill \cr} \right.;\,\,y\left( { - 1} \right) = 3;\,y\left( 1 \right) = - 1 \cr} \)
Bảng biến thiên:

\(y'' = 6x;\,y'' = 0 \Leftrightarrow x = 0;\,y\left( 0 \right) = 1\)
Xét dấu \(y”\)

Điểm uốn \(I(0;1)\)
Điểm đặc biệt:\(x = 2 \Rightarrow y = 3\)
Đồ thị: Đồ thị nhận \(I(0;1)\) làm tâm đối xứng.
c) TXĐ: \(D =\mathbb R\)
\(\mathop {\lim }\limits_{x \to + \infty } y = - \infty ;\,\,\mathop {\lim }\limits_{x \to - \infty } y = + \infty \)
\(y' = - {x^2} + 2x - 2 < 0\) với mọi \(x \in\mathbb R\)
Hàm số nghịch biến trên \(\mathbb R\)
Bảng biến thiên:

\(y'' = - 2x + 2;\,y'' = 0 \Leftrightarrow x = 1;\,y\left( 1 \right) = - 2\)
Xét dấu \(y”\)
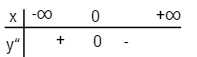
Điểm uốn \(I(1;-2)\)
Điểm đặc biết:\(x = 0 \Rightarrow y = {{ - 2} \over 3}\)
Đồ thị: Đồ thị nhận \(I(1;-2)\) làm tâm đối xứng.
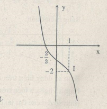
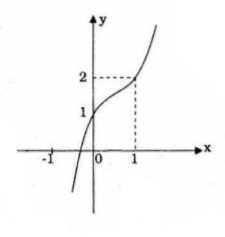
d) TXĐ: \(D =\mathbb R\)
\(\mathop {\lim }\limits_{x \to + \infty } y = + \infty ;\,\mathop {\lim }\limits_{x \to - \infty } y = - \infty \)
\(y' = 3{x^2} - 6x + 3 = 3{\left( {x - 1} \right)^2} \ge 0\) với mọi \(x \in\mathbb R\)
Dấu bằng chỉ xảy ra khi \(x = 1\)
Hàm số đồng biến trên \(\mathbb R\)
Bảng biến thiên:
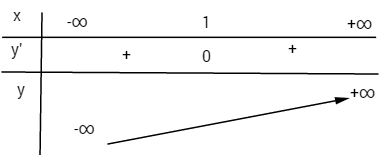
Xét dấu \(y”\)

Điểm uốn \(I(1;2)\)
Điểm đặc biệt: \(x = 0 \Rightarrow y = 1\)
Đồ thị: Đồ thị nhận \(I(1;2)\) làm tâm đối xứng.