Nội dung bài giảng
Cho số phức \({\rm{w}} = \bar z{{1 - 3i} \over {1 + 2i}},\) trong đó \(z = \cos \varphi + i\sin \varphi ,\left( {\varphi \in R} \right)\)
a) Hãy viết số phức w dưới dạng lượng giác.
b) Xác định tập hợp các điểm trong mặt phẳng phức biểu diễn các số phức w nói trên khi \(\varphi \)) thay đổi, \(0 \le \varphi \le \pi \)
Giải
a) Ta có \(\bar z = \cos \varphi - i\sin \varphi = \cos \left( { - \varphi } \right) + i\sin \left( { - \varphi } \right),\)
\({{1 - 3i} \over {1 + 2i}} = - \left( {1 + i} \right) = \sqrt 2 \left( {\cos {{5\pi } \over 4} + i\sin {{5\pi } \over 4}} \right)\)
Vậy \({\rm{w}} = \bar z{{1 - 3i} \over {1 + 2i}} = \sqrt 2 \left[ {\cos \left( {{{5\pi } \over 4} - \varphi } \right) + i\sin \left( {{{5\pi } \over 4} - \varphi } \right)} \right]\)
b) Do \(0 \le \varphi \le \pi \) nên \({\pi \over 4} \le {{5\pi } \over 4} - \varphi \le {{5\pi } \over 4}.\)
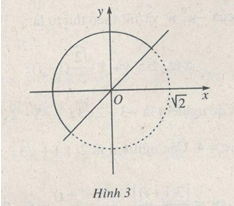
Vậy tập hợp cần tìm là nửa đường tròn tâm O, bán kính bằng \(\sqrt 2 \), nằm phía trên đường phân giác của góc phần tư thứ nhất của hệ tọa độ. (h.3)