Nội dung bài giảng
Câu III.1 Trang 114 Sách Bài Tập (SBT) Toán 9 Tập 2
Cho tam giác đều ACB và ACD, cạnh a. Lần lượt lấy B và D làm tâm vẽ hai đường tròn bán kính a. Kẻ các đường kính ABE và ADF. Trên cung nhỏ CE của đường tròn tâm B lấy điểm M (không trùng với E và C). Đường thẳn CM cắt đường tròn tâm D tại điểm thứ hai là N. Hai đường thẳng EM và NF cắt nhau tại điểm T. Gọi H là giao điểm của AT và MN.
Chứng minh:
a) MNT là tam giác đều.
b) AT = 4AH.
Giải

a) Trong đường tròn (B) ta có:
\(\widehat {AMC} = {1 \over 2}\widehat {ABC}\) (hệ quả góc nội tiếp) mà \(\widehat {ABC} = 60^\circ \) (vì ∆ABC đều)
\( \Rightarrow \widehat {AMC} = 30^\circ \)
\(\widehat {AME} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn (B))
\( \Rightarrow \widehat {AMT} = 90^\circ \)
\(\widehat {TMN} = \widehat {AMT} - \widehat {AMC} = 90^\circ - 30^\circ = 60^\circ \)
Trong đường tròn (D) ta có:
\(\widehat {ANC} = {1 \over 2}\widehat {ADC}\) (Hệ quả góc nội tiếp) mà \(\widehat {ADC} = 60^\circ \) (vì ∆ADC đều) \( \Rightarrow \widehat {ANC} = 30^\circ \)
\(\widehat {ANF} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn (D))
\( \Rightarrow \widehat {ANC} + \widehat {CNF} = 90^\circ \Rightarrow \widehat {CNF} = 90^\circ - \widehat {ANC} = 90^\circ - 30^\circ = 60^\circ \) hay \(\widehat {MNT} = 60^\circ \)
Vậy ∆TMN đều.
b) \(\widehat {AMC} = \widehat {ANC} = 30^\circ \)
\( \Rightarrow \Delta AMN\) cân tại A \( \Rightarrow \) AM = AN nên A nằm trên đường trung trực MN ∆TMN đều
\( \Rightarrow \) TM = TN nên T nằm trên đường trung trực MN
Suy ra AT là đường trung trực của MN nên AT ⊥ MN
∆AHM có \(\widehat {AHM} = 90^\circ \)
\(AM = {{AH} \over {\sin M}} = {{AH} \over {\sin 30^\circ }} = {{AH} \over {{1 \over 2}}} = 2AH\) (1)
TH ⊥ MN nên TH là đường phân giác của \(\widehat T\) nên \(\widehat {MTA} = 30^\circ \)
∆AMT có \(\widehat {AMT} = 90^\circ \)
\(AT = {{AT} \over {\sin \widehat {MTA}}} = {{AM} \over {{1 \over 2}}} = 2AM\) (2)
Từ (1) và (2) suy ra: AT = 4AH
Câu III.2 trang 115 Sách Bài Tập (SBT) Toán 9 Tập 2
Cho đường tròn tâm O bán kính R và điểm M ở ngoài đường tròn đó. Qua điểm M kẻ hai tiếp tuyến MA, MB và cắt tuyến MCD với đường tròn (O), trong đó điểm C ở giữa hai điểm M, D. Đường thẳng qua điểm C và vuông góc với OA cắt AB tại H. Gọi I là trung điểm của dây CD. Chứng minh HI song song với AD.
Giải
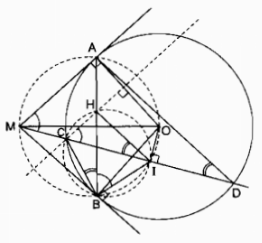
MA ⊥ OA (tính chất tiếp tuyến)
\( \Rightarrow \widehat {MAO} = 90^\circ \)
MB ⊥ OB (tính chất tiếp tuyến)
\( \Rightarrow \widehat {MBO} = 90^\circ \)
IC = ID (gt)
\( \Rightarrow \) OI ⊥ CD (đường kính đi qua điểm chính giữa của dây)
\( \Rightarrow \widehat {MIO} = 90^\circ \)
A, B, I nhìn MO cố định dưới một góc bằng 90º nên A, B, I nằm trên đường tròn bán kính MO.
\( \Rightarrow \widehat {AMI} = \widehat {ABI}\) (Hai góc nội tiếp cùng chắn cung nhỏ AOI)
CH ⊥ \(\overparen{AO}\) (gt)
Suy ra: CH // MA
\(\widehat {AMI} = \widehat {HCI}\) (hai góc đồng vị)
Suy ra: \(\widehat {HCI} = \widehat {ABI}\) hay \(\widehat {HCI} = \widehat {HBI}\)
B và C cùng nằm trên một nửa mặt phẳng bờ chứa đường HI tạo với HI một góc bằng nhau nên tứ giác BCHI nội tiếp.
\( \Rightarrow \widehat {CBH} = \widehat {CIH}\) (hai góc nội tiếp cùng chắn cung nhỏ \(\overparen{CH}\)) hay \(\widehat {CBA} = \widehat {CIH}\) (1)
Trong đường tròn (O) ta có:
\(\widehat {CBA} = \widehat {CDA}\) (2 góc nội tiếp cùng chắn cung nhỏ \(\overparen{AC}\) (2)
Từ (1) và (2) suy ra: \(\widehat {CIH} = \widehat {CDA}\) nên HI // AD (vì có cặp góc ở vị trí đồng vị bằng nhau)
(Trường hợp cát tuyến đi qua tâm ngũ giác MAOIB suy biến thành tứ giác MAOB chứng minh tương tự ta có HO // AD).

