Biết n là số nguyên dương thỏa mãn \(C_{n}^{n-1}+C_{n}^{n-2}=78\). Số hạng chứa \({{x}^{4}}\) trong khai triển \({{\left( {{x}^{3}}-\frac{2}{x} \right)}^{n}}\) là
\(C_{n}^{n-1}+C_{n}^{n-2}=78\Leftrightarrow \frac{n!}{1!(n-1)!}+\frac{n!}{2!(n-2)!}=78\Leftrightarrow n+\frac{1}{2}n(n-1)=78\Leftrightarrow 2n+{{n}^{2}}-n-156=0\Leftrightarrow {{n}^{2}}+n-156=0\)
\(\Leftrightarrow \left[ \begin{align} & n=-13\,\,(L) \\ & n=12\,\,(TM) \\\end{align} \right.\)
Khi đó, \({{\left( {{x}^{3}}-\frac{2}{x} \right)}^{n}}={{\left( {{x}^{3}}-\frac{2}{x} \right)}^{12}}=\sum\limits_{i=0}^{12}{C_{12}^{i}{{x}^{3i}}.{{\left( -2{{x}^{-1}} \right)}^{12-i}}}=\sum\limits_{i=0}^{12}{C_{12}^{i}{{\left( -2 \right)}^{12-i}}{{x}^{4i-12}}}\)
Số hạng \({{x}^{4}}\) trong khai triển tương ứng với i thỏa mãn: \(4i-12=4\Leftrightarrow i=4\)
Vậy số hạng chứa \({{x}^{4}}\) trong khai triển \({{\left( {{x}^{3}}-\frac{2}{x} \right)}^{12}}\)là \(C_{12}^{4}{{\left( -2 \right)}^{8}}{{x}^{4}}=\) \(126\,720{{x}^{4}}\)
Chọn: A

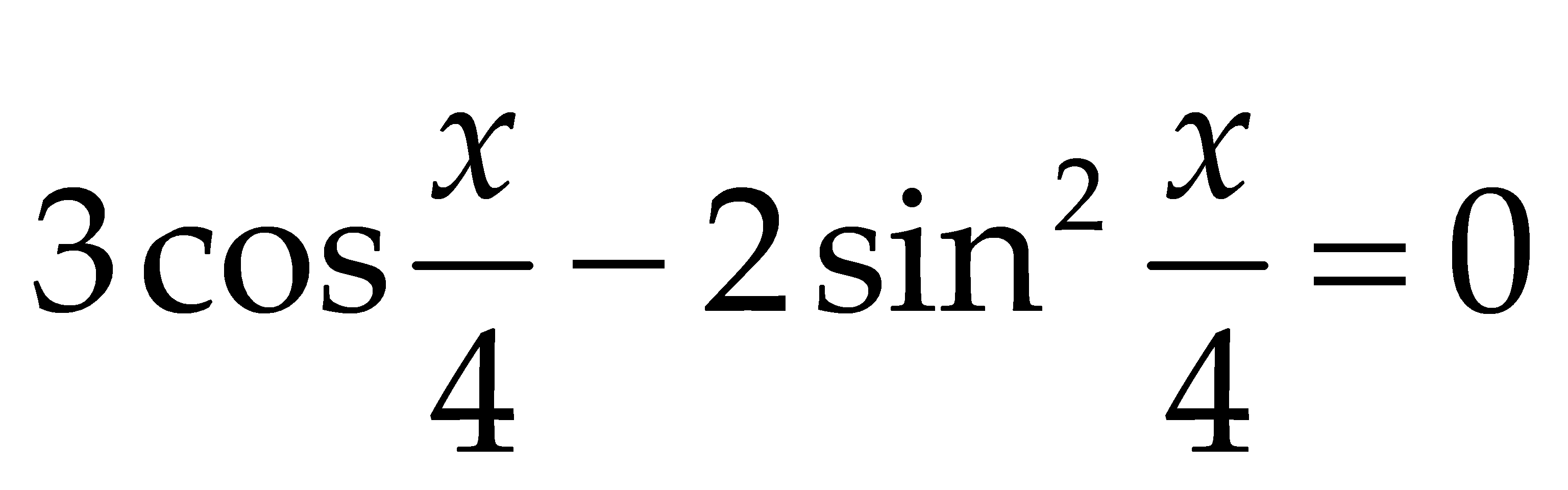 trên đoạn
trên đoạn