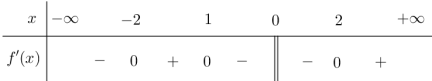Biết phương trình \({{\log }_{5}}\frac{2\sqrt{x}+1}{x}=2{{\log }_{3}}\left( \frac{\sqrt{x}}{2}-\frac{1}{2\sqrt{x}} \right)\) có một nghiệm dạng \(x=a+b\sqrt{2}\) trong đó a,b là các số nguyên. Tính 2a + b.
ĐkXĐ: x > 1
Ta có
\(\begin{array}{l} {\log _5}\frac{{2\sqrt x + 1}}{x} = 2{\log _3}\left( {\frac{{\sqrt x }}{2} - \frac{1}{{2\sqrt x }}} \right) \Leftrightarrow {\log _5}\frac{{2\sqrt x + 1}}{x} = 2{\log _3}\left( {\frac{{x - 1}}{{2\sqrt x }}} \right)\\ \Leftrightarrow {\log _5}\left( {2\sqrt x + 1} \right) - {\log _5}x = 2{\log _3}\left( {x - 1} \right) - 2{\log _3}\left( {2\sqrt x } \right)\\ \Leftrightarrow {\log _5}\left( {2\sqrt x + 1} \right) + 2{\log _3}\left( {2\sqrt x } \right) = {\log _5}x + 2{\log _3}\left( {x - 1} \right)\,\,\,\,(1) \end{array}\)
Xét hàm số \(f\left( t \right)={{\log }_{5}}t+2{{\log }_{3}}\left( t-1 \right),t\in \left( 1;+\infty \right)\), có:\(f'\left( t \right)=\frac{1}{t.\ln 5}+\frac{2}{\left( t-1 \right).\ln 3}>0,\forall t\in (1;+\infty )\)
⇒ Hàm số \(f\left( t \right)\) đồng biến trên \(\left( 1;+\infty \right)\)
Khi đó, phương trình
\(\left( 1 \right) \Leftrightarrow f\left( {2\sqrt x + 1} \right) = f\left( x \right) \Leftrightarrow 2\sqrt x + 1 = x \Leftrightarrow x - 2\sqrt x - 1 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {\sqrt x = 1 + \sqrt 2 }\\ {\sqrt x = 1 - \sqrt 2 < 0} \end{array}} \right.\)
\( \Leftrightarrow \sqrt x = 1 + \sqrt 2 \Leftrightarrow x = {\left( {1 + \sqrt 2 } \right)^2} = 3 + 2\sqrt 2 \Rightarrow a = 3,b = 2 = > 2a + b = 2.3 + 2 = 8\)

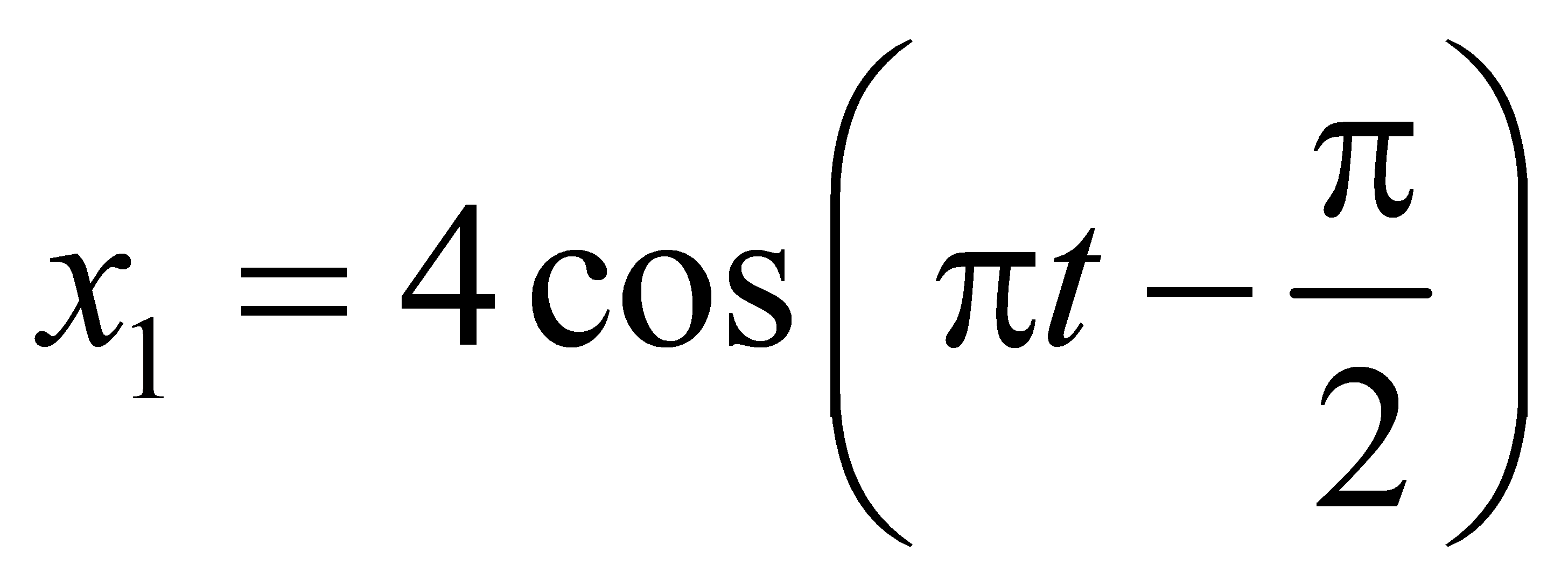 cm ,
cm , 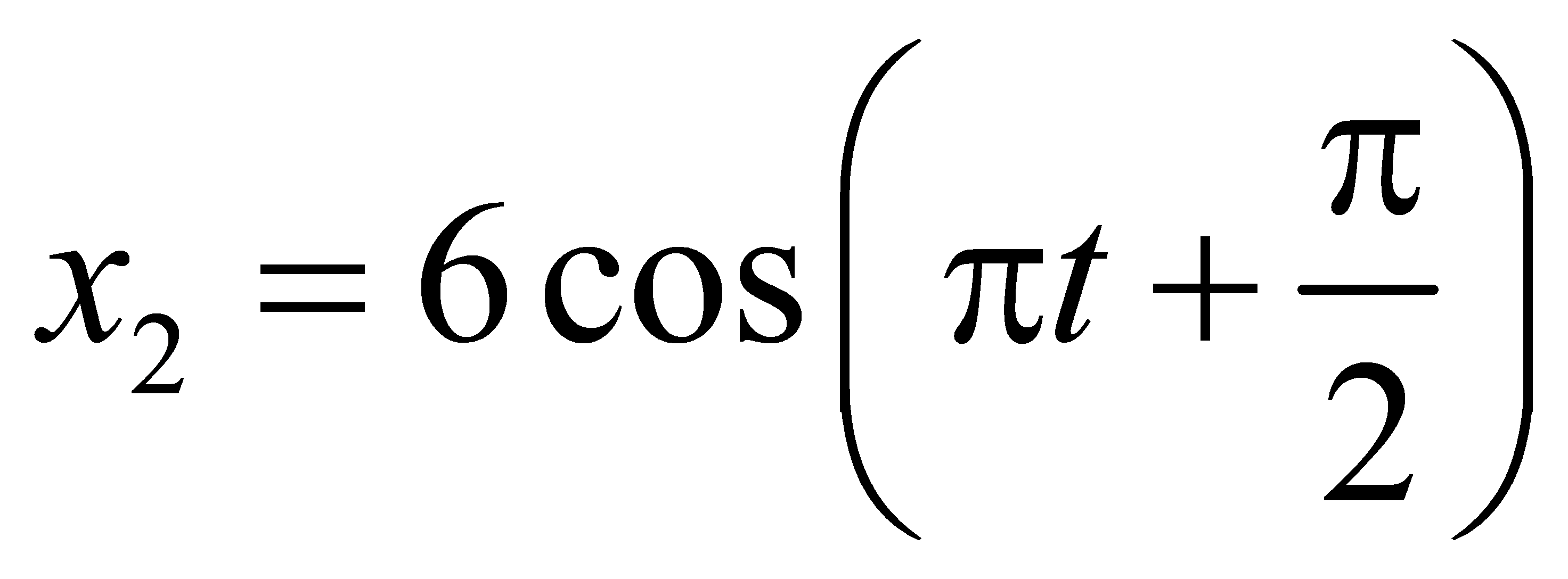 cm và
cm và