Cho (A ) là điểm cố định trên đường tròn (O;R) Gọi AB và AC là hai dây cung thay đổi trên đường tròn (O ) thỏa mãn \( \sqrt {AB.AC} = R\sqrt 3 ,\) Khi đó vị trí của (B,C ) trên ( O ) để diện tích tam gíac ABC lớn nhất là:
Kẻ AH⊥BC,OI⊥BC, đường kính AD.
Ta chứng minh được ΔAHC∽ΔABD(g−g).
Do đó \( \frac{{AH}}{{AB}} = \frac{{AC}}{{AD}} \Rightarrow AH.AD = AB.AC \Rightarrow AB.AC = 2R.AH{\mkern 1mu} {\mkern 1mu} \left( 1 \right).\)
Theo giả thiết \( \sqrt {AB.AC} = R\sqrt 3 ,\) nên \( AB.AC = 3{R^2}{\mkern 1mu} {\mkern 1mu} \left( 2 \right).\)
Thay (2) và (1) ta có \( AH = \frac{{3R}}{2}.\)
Lại có \( OI + OA \ge AI \ge AH \to OI \ge AH - OA = \frac{{3R}}{2} - R = \frac{R}{2}.\)
Do \( AH = \frac{{3R}}{2}\) là giá trị không đổi nên SABC lớn nhất khi BC lớn nhất ⇔OI nhỏ nhất
\( \Leftrightarrow OI = \frac{R}{2} \Leftrightarrow BC \bot OA \Rightarrow {\rm{\Delta }}ABC\) cân tại A
Mà
\(\begin{array}{l} OI = \frac{R}{2} \Rightarrow \sin \widehat {OBI} = \frac{{OI}}{{OB}} = \frac{1}{2} \Rightarrow \widehat {OBI} = \widehat {OCI} = {30^0} \Rightarrow \widehat {BOC} = {120^0}\\ \Rightarrow \widehat {BAC} = {60^0} \end{array}\)
Vậy ΔABC đều.

.JPG)
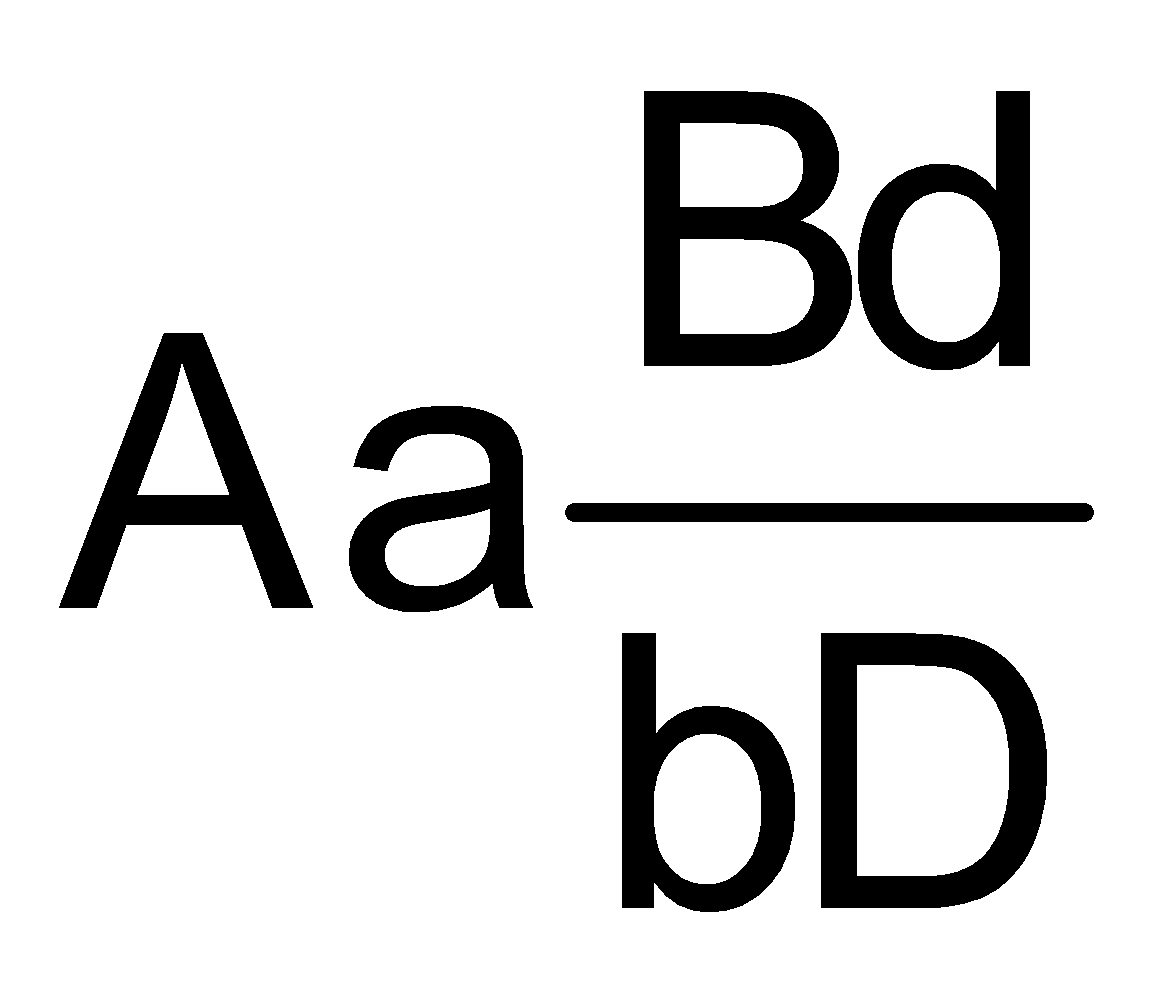 lai phân tích. Kết luận nào sau đây đúng?
lai phân tích. Kết luận nào sau đây đúng?