Cho hàm số $f(x)$ thỏa mãn $[xf'(x)]^2+1=x^2[1-f(x).f''(x)]$ với mọi $x$ dương. Biết $f(1)=f'(1)=1$. Tính $f^2(2)$.
A.
$f^2(2)=2ln2+2$.
B.
$f^2(2)=\sqrt{ln2+1}$.
C.
$f^2(2)=\sqrt{2ln2+2}$.
D.
$f^2(2)=ln2+1$.
Đáp án và lời giải
Đáp án:A
Lời giải:Ta có: $[xf'(x)]^2+1=x^2[1-f(x).f''(x)]$ $\Leftrightarrow$$x^2[(f'(x))^2+f(x).f''(x)]=x^2-1$ $$\Leftrightarrow(f'(x))^2+f(x).f''(x)=1-\frac{1}{x^2}\Rightarrow\int[(f'(x))^2+f(x).f''(x)]dx=\int(1-\frac{1}{x^2})dx (*)$$Do $(f(x).f'(x))'=f'(x).f'(x)+f(x).f''(x)=(f'(x))^2+f(x).f''(x)$ nên từ (*), ta suy ra được: $f(x).f'(x)=x+\frac{1}{x}+C(**)$; mặt khác $f(1)=f'(1)=1$ thay vào (**) ta tìm được $C=-1$.Vậy, ta tìm được $f(x).f'(x)=x+\frac{1}{x}-1$$$\Rightarrow\int_1^2 f(x).f'(x)dx=\int_1^2 (x+\frac{1}{x}-1)dx\Rightarrow\int_1^2 f(x)d(f(x))=(\frac{x^2}{2}+ln|x|-x)|_1^2$$$\Rightarrow\frac{f^2(x)}{2}|_1^2=ln2+\frac{1}{2}\Rightarrow\frac{f^2(2)}{2}-\frac{f^2(1)}{2}=ln2+\frac{1}{2}\Rightarrow$$f^2(2)=2ln2+2$ (do $f(1)=1$)


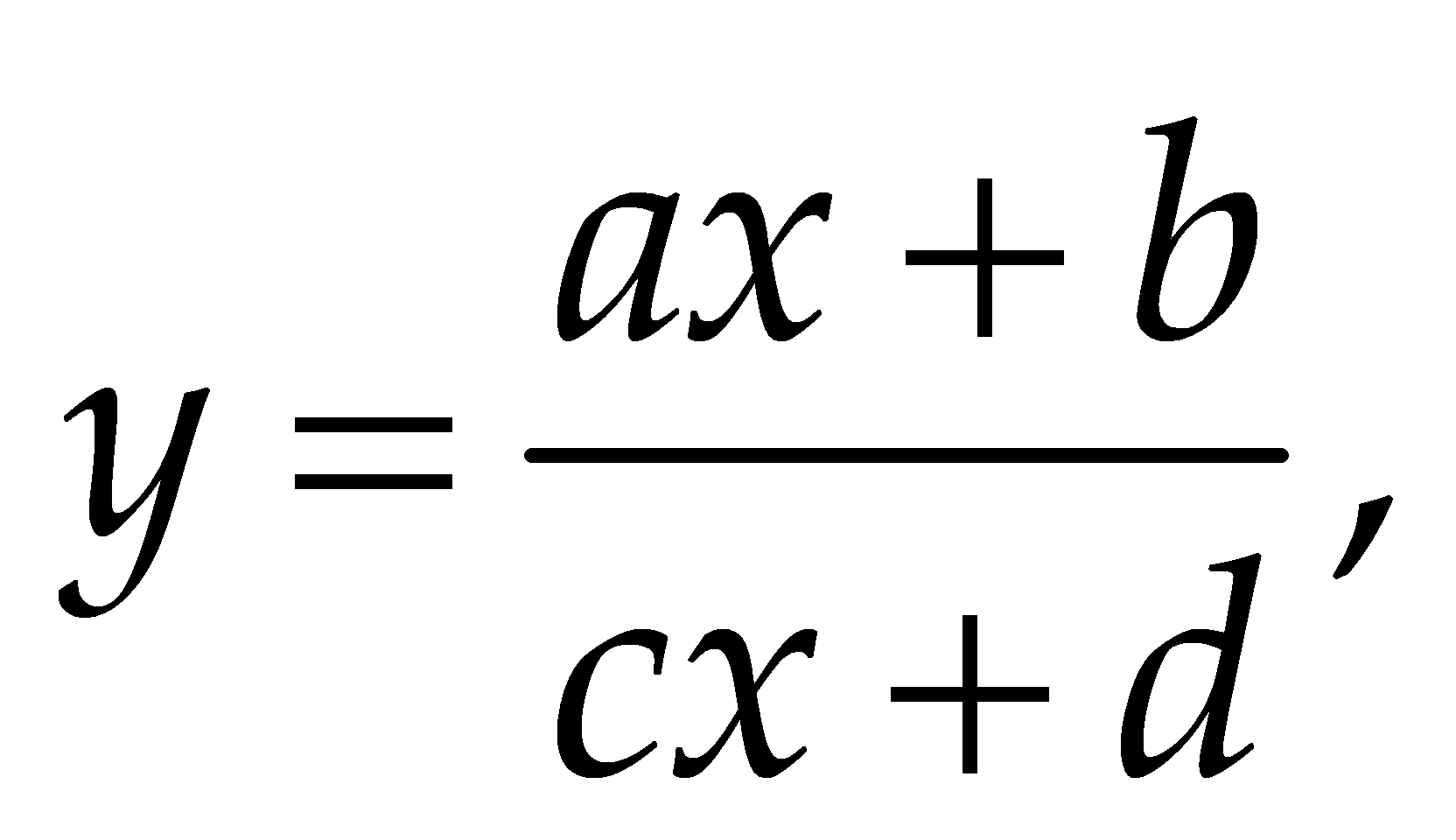 với
với