Đồ thị hàm số có mấy đường tiệm cận?
A. .
B. .
C. .
D. .
Đáp án và lời giải
Đáp án:B
Lời giải:Lời giải
Chọn B
Ta có: ; nên đồ thị hàm số nhận đường thẳng là tiệm cận ngang.
; nên đồ thị hàm số nhận đường thẳng là tiệm cận đứng.
; nên đồ thị hàm số nhận đường thẳng là tiệm cận đứng.
Vậy đồ thị hàm số đã cho có đường tiệm cận.
Chọn B
Ta có: ; nên đồ thị hàm số nhận đường thẳng là tiệm cận ngang.
; nên đồ thị hàm số nhận đường thẳng là tiệm cận đứng.
; nên đồ thị hàm số nhận đường thẳng là tiệm cận đứng.
Vậy đồ thị hàm số đã cho có đường tiệm cận.
Vậy đáp án đúng là B.

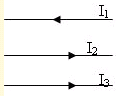 Có 3 dòng điện thẳng song song I1, I2 và I3 ở trong cùng một mặt phẳng, cho I1 = 20 A, I2 = 15 A, I3 = 25 A. Khoảng cách giữa I1, I2 là a = 5 cm, giữa I2 và I3 là b = 3 cm. Lực tác dụng lên 1 m chiều dài của I3 là
Có 3 dòng điện thẳng song song I1, I2 và I3 ở trong cùng một mặt phẳng, cho I1 = 20 A, I2 = 15 A, I3 = 25 A. Khoảng cách giữa I1, I2 là a = 5 cm, giữa I2 và I3 là b = 3 cm. Lực tác dụng lên 1 m chiều dài của I3 là