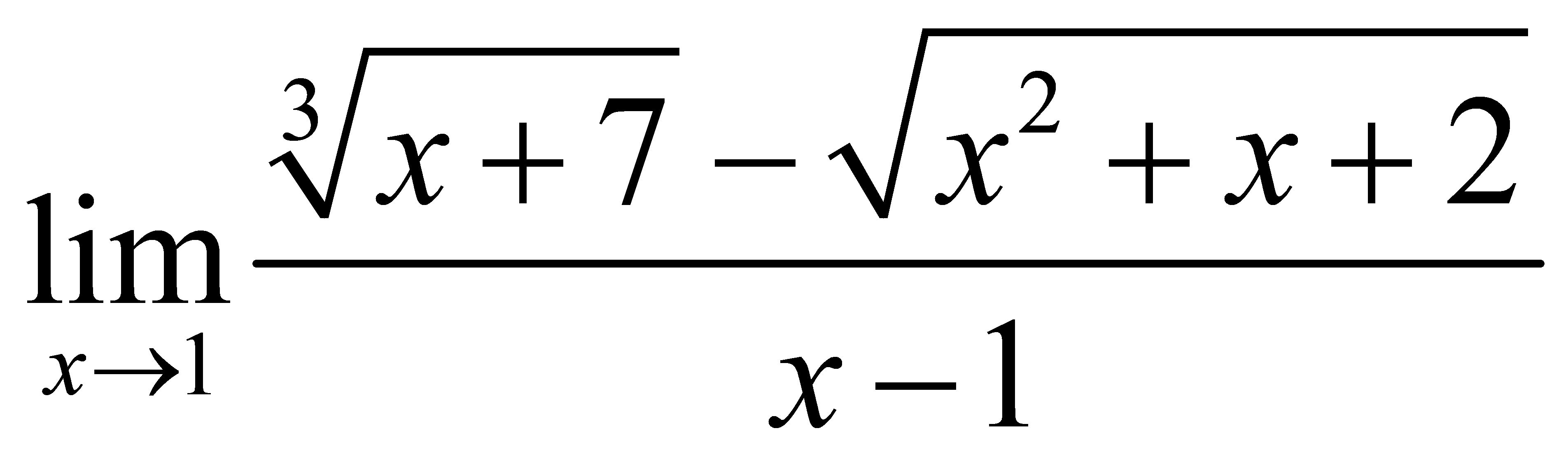Họ nguyên hàm của hàm số là
A. .
B. .
C. .
D. .
Đáp án và lời giải
Đáp án:C
Lời giải:Lời giải
Chọn C
Ta có: .
. Đặt .
.
.
Chọn C
Ta có: .
. Đặt .
.
.
Vậy đáp án đúng là C.

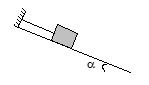 đường dốc chính. Biết α = 300. Cho g = 9,8 m/s2. Lực căng T của dây treo là
đường dốc chính. Biết α = 300. Cho g = 9,8 m/s2. Lực căng T của dây treo là