Trong không gian Oxyz, cho điểm \(M\left( 1;1;1 \right)\). Mặt phẳng \(\left( P \right)\) đi qua M và cắt chiều dương của các trục Ox,Oy,Oz lần lượt tại các điểm \(A\left( a;0;0 \right),B\left( 0;b;0 \right),C\left( 0;0;c \right)\) thỏa mãn OA=2OB và thể tích khối tứ diện OABC đạt giá trị nhỏ nhất. Tính S=2a+b+3c.
Phương trình mặt phẳng \(\left( P \right)\) đi qua \(A\left( a;0;0 \right),B\left( 0;b;0 \right),C\left( 0;0;c \right)\) có dạng \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1.\)
Vì \(\left( P \right)\) đi qua M nên \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=1.\)
Mặt khác OA=2OB nên a=2b nên \(\frac{3}{2b}+\frac{1}{c}=1.\)
Thể tích khối tứ diện OABC là \(V=\frac{1}{6}abc=\frac{1}{3}{{b}^{2}}c.\)
Ta có \(\frac{3}{2b}+\frac{1}{c}=\frac{3}{4b}+\frac{3}{4b}+\frac{1}{c}\ge 3\sqrt[3]{\frac{9}{16{{b}^{2}}c}}\Rightarrow \sqrt[3]{\frac{9}{16{{b}^{2}}c}}\le \frac{1}{3}\Rightarrow \frac{16{{b}^{2}}c}{9}\ge 27\Rightarrow V=\frac{{{b}^{2}}c}{3}\ge \frac{81}{16}.\)
\(\Rightarrow \min V=\frac{81}{16} \ khi \ \left\{ \begin{align} & \frac{3}{4b}=\frac{1}{c}=\frac{1}{3} \\ & a=2b \\ \end{align} \right.\)\(\Rightarrow \left\{ \begin{align} & a=\frac{9}{2} \\ & b=\frac{9}{4} \\ & c=3 \\ \end{align} \right..\)
Vậy \(S=2a+b+3c=\frac{81}{4}.\)

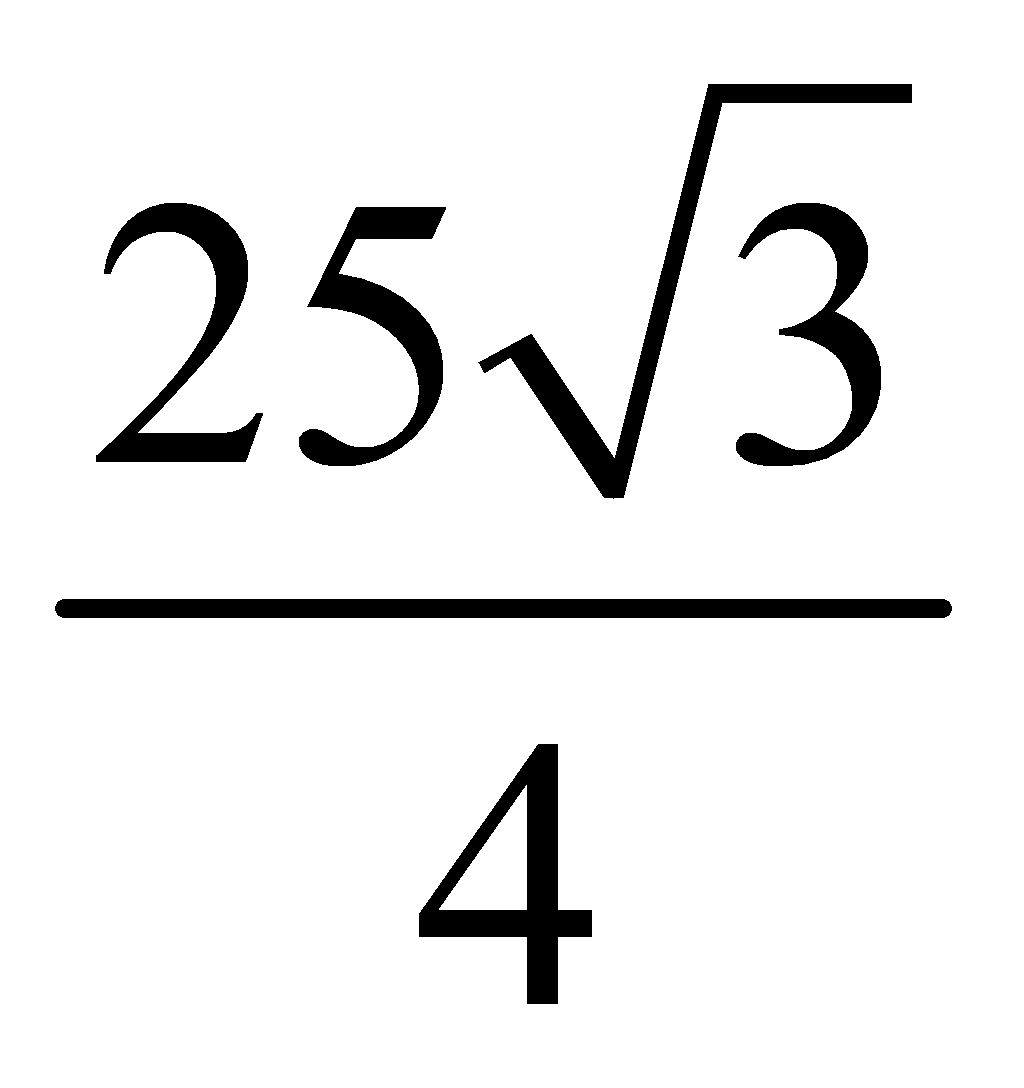 N là 0,1 s. Quãng đường lớn nhất mà vật nhỏ của con lắc đi được trong 0,4 s gần giá trị nào nhất sau đây?
N là 0,1 s. Quãng đường lớn nhất mà vật nhỏ của con lắc đi được trong 0,4 s gần giá trị nào nhất sau đây?