Xét các số thực dương x, y thỏa mãn \({\log _3}\frac{{1 - xy}}{{x + 2y}} = 3xy + x + 2y - 4.\) Tìm giá trị nhỏ nhất \({P_{\min }}\) của \(P = x + y.\)
\(\begin{array}{l}
{\log _3}\frac{{1 - xy}}{{x + 2y}} = 3xy + x + 2y - 4\\
\Leftrightarrow {\log _3}\left( {1 - xy} \right) - {\log _3}\left( {x + 2y} \right)\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\, = - 3\left( {1 - xy} \right) + x + 2y - 1\\
\Leftrightarrow {\log _3}3\left( {1 - xy} \right) + 3\left( {1 - xy} \right)\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {\log _3}\left( {x + 2y} \right) + \left( {x + 2y} \right)
\end{array}\)
Xét hàm số \(f\left( t \right) = {\log _3}t + t\,\left( {t > 0} \right)\), ta có:
\(f'\left( t \right) = \frac{1}{{t\ln 3}} + 1 > 0,\forall t > 0\)
Suy ra hàm số \(f(t)\) đồng biến trên khoảng \(\left( {0; + \infty } \right)\)
Do đó \(f\left( {3 - 3xy} \right) = f\left( {x + 2y} \right)\)
\(\begin{array}{l}
\Leftrightarrow 3 - 3xy = x + 2y\\
\Leftrightarrow 3 - x = y\left( {3x + 2} \right)
\end{array}\)
Khi đó \(y = \frac{{3 - x}}{{3x + 2}}\)
\(\begin{array}{l}
\Rightarrow P = x + \frac{{3 - x}}{{3x + 2}}\\
\Rightarrow P' = 1 - \frac{{11}}{{{{\left( {3x + 2} \right)}^2}}} = 0\\
\Rightarrow x = \frac{{\sqrt {11} - 2}}{3}\left( {x > 0} \right)
\end{array}\)
\({P_{\min }} = P\left( {\frac{{\sqrt {11} - 2}}{3}} \right) = \frac{{2\sqrt {11} - 3}}{3}\)
Chọn A.

 là:
là:  có đồ thị
có đồ thị 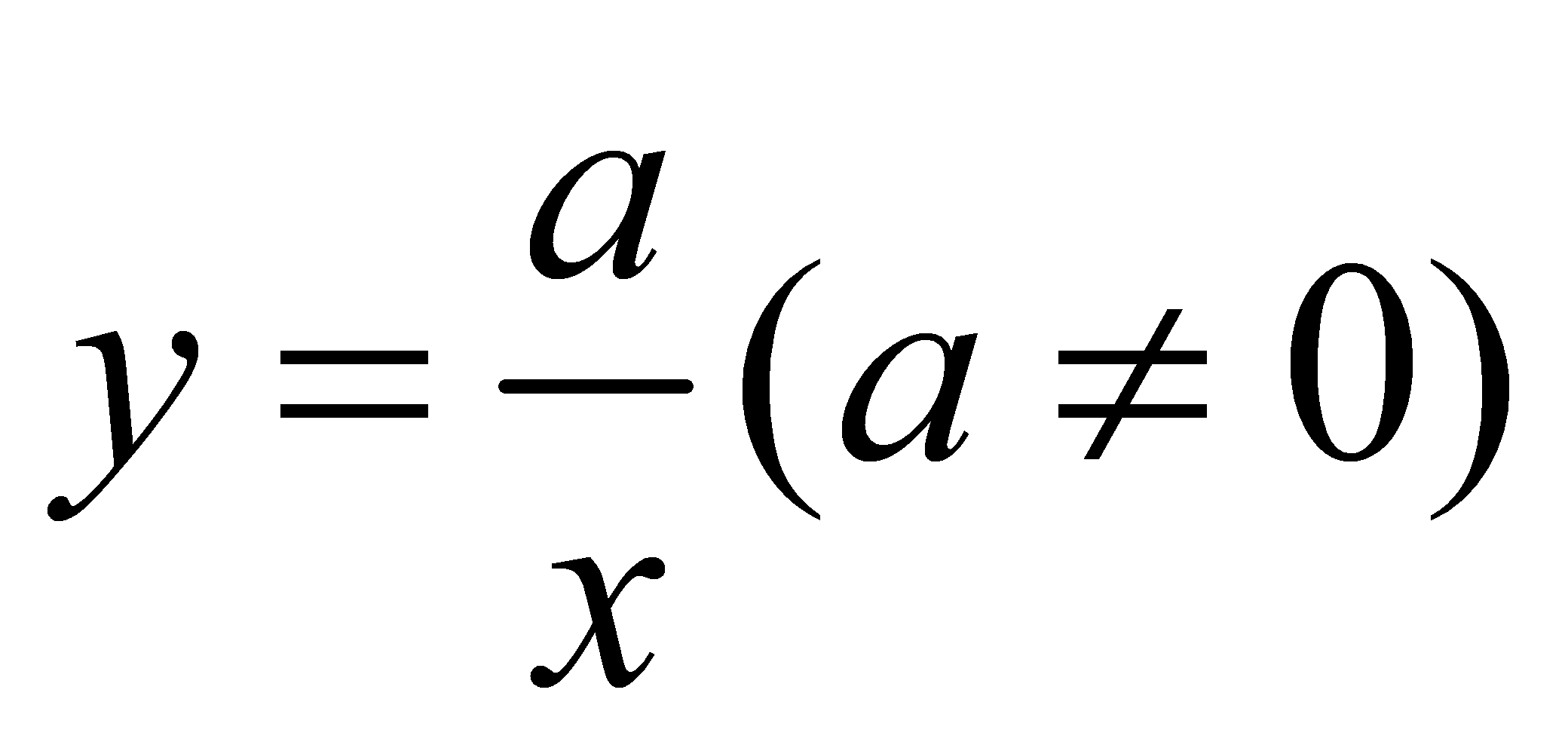 có đồ thị (H). Gọi d là khoảng cách từ giao điểm hai tiệm cận của đồ thị (H) đến một tiếp tuyến của (H). Giá trị lớn nhất của d có thể đạt được là:
có đồ thị (H). Gọi d là khoảng cách từ giao điểm hai tiệm cận của đồ thị (H) đến một tiếp tuyến của (H). Giá trị lớn nhất của d có thể đạt được là: