Nội dung bài giảng
Cho điểm A cách đường thẳng xy là 12cm. Vẽ đường tròn (A ; 13cm).
a) Chứng minh rằng đường tròn (A) có hai giao điểm với đường thẳng xy.
b) Gọi hai giao điểm nói trên là B và C. Tính độ dài BC.
Giải:
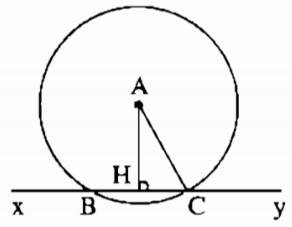
a) Kẻ AH ⊥ xy
Ta có: AH = 12cm
Bán kính đường tròn tâm I là 13cm nên R = 13cm.
Mà AH = d = 12cm
Nên suy ra d < R
Vậy ( A; 13cm) cắt đường thẳng xy tại hai điểm phân biệt B và C.
b) Áp dụng định lí Pi-ta-go vào tam giác vuông AHC, ta có:
\(A{C^2} = A{H^2} + H{C^2}\)
Suy ra: \(H{C^2} = A{C^2} - A{H^2} = {13^2} - {12^2} = 25 \Rightarrow HC = 5(cm)\)
Ta có: BC = 2.HC = 2.5 = 10 (cm)

