Nội dung bài giảng
Trên một đường tròn, có cung AB bằng 1400, cung AD nhận B làm điểm chính giữa, cung CB nhận A là điểm chính giữa. Tính số đo cung nhỏ CD và cung lớn CD.
Giải
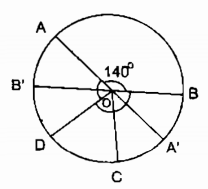
Ta có: cung AB = cung BD = cung AC (gt)
\( \Rightarrow \widehat {AOB} = \widehat {BOD} = \widehat {AOC} = {180^0}\)
Kẻ đường kính AA’, BB’ ta có:
\(\widehat {AOB} + \widehat {AOB'} = {180^0}\) (hai góc kề bù)
\( \Rightarrow \widehat {AOB'} = {180^0} - \widehat {AOB} = {180^0} - {140^0} = {40^0}\)
Suy ra: \(\widehat {BOA'} = \widehat {AOB'} = {40^0}\) (hai góc đối đỉnh)
\(\widehat {B'OD} + \widehat {BOD} = {180^0}\) (hai góc kề bù)
\( \Rightarrow \widehat {B'OD} = {180^0} - \widehat {BOD} = {180^0} - {140^0} = {40^0}\)
\(\widehat {AOC} = \widehat {AOB'} + \widehat {B'OD} + \widehat {DOC}\)
\( \Rightarrow \widehat {DOC} = \widehat {AOC} - \widehat {AOB'} - \widehat {B'OD} = {140^0} - {40^0} - {40^0} = {60^0}\)
sđ cung CD (nhỏ) = \(\widehat {COD} = {60^0}\)
sđ cung CD (lớn) = sđ cung CD (nhỏ) = 3600 – 600 = 3000

